تصحيح الموحد لنيل شهادة السلك الإعدادي مادة الرياضيات يونيو 2009

byذ. البشير الصالحي -
0

تمارين وأنشطة الامتحان الجهوي الموحد لنيل شهادة السلك الإعدادي مادة الرياضيات مرفقة بالتصحيح.

الامتحان الجهوي الموحد لجهة تازة المستوى الثالثة اعدادي

 نعرض في هذه التدوينة نموذج الامتحان الموحد لجهة تازة دورة يونيو 2009 ( الإمتحان الجهوي )، وهي فرصة لتلامذة المستوى الثالث اعدادي مع التصحيح.


تصحيح الموحد لنيل شهادة السلك

التمرين 1

تصحيح التمرين 1 ويتضمن حلا لمعدلتين، حلا لمتراجحتين وحلا جبريا لنظمتين.

التمرين 1

1) حل المعادلتين:     
  • أ- \( 5x-2=3x+4\)
  • ب- \( (2x+6)^{2}-x^{2}=0\)
2) حل المتراجحتين:
  • أ-\( 5x+15\leqslant 5\)
  • ب- \( 2x+5> 6(x+1)+3\)
3) حل جبريا النظمتين التاليتين:
  • أ- \( \left\{\begin{matrix} 3x+y&=3 \\ x-y&=5 \\\end{matrix}\right.\)
  • ب- \( \left\{\begin{matrix} \frac{x+2}{3}&=y \\ 2x-3y&=2 \\\end{matrix}\right.\)
تصحيح التمرين 1
1) حل المعادلتين:     
  • أ- \( 5x-2=3x+4\) \[5x-3x-2=4+2\]\[\Rightarrow 2x=6\Rightarrow x=3\]
الحل:     \(x=3\)
  • ب- \( (2x+6)^{2}-x^{2}=0\)
\[(2x+6)^{2}-x^{2}=0\]\[\Rightarrow((2x+6)-x)((2x+6)+x)=0\]\[(2x+6)-x=0\Rightarrow x=-6 \]\[(2x+6)+x=0\Rightarrow 3x=-6 \]\[\Rightarrow x=-2 \]
الحل:     \(x=-2;x=-6 \)
2) حل المتراجحتين:
  • أ-\( 5x+15\leqslant 5\)
\[5x+15\leqslant 5\Rightarrow  \]\[5x\leqslant 5-15\Rightarrow 5x\leqslant-10 \]\[ x\leqslant-2 \]
الحل:     \( x\leqslant-2 \)

  • ب- \( 2x+5> 6(x+1)+3\)
\[ 2x+5>6(x+1)+3 \]\[ \Rightarrow 2x-6x>6+3-5 \]\[ \Rightarrow-4x>4\Rightarrow x<-1 \]
الحل:     \( x<-1 \)
3) حل جبريا النظمتين التاليتين:
  • أ- \(\left\{\begin{matrix}3x+y=3&\\x-y=5&\\\end{matrix}\right.\)
\[3x-3x+y-(-3y)=3-15 \]\[4y=-12 \]\[ \Rightarrow y=-3 \]\[ \Rightarrow 3x-3=3 \]\[ \Rightarrow x=2 \]
الحل:      \((x;y)=(2;-3)\)

ب-    \( \left\{\begin{matrix} \frac{x+2}{3}&=y \\ 2x-3y&=2 \\\end{matrix}\right.\)
\[(1)-(2)\Rightarrow \]\[x-2x+2+3y=3y-2\]\[\Rightarrow x=4\]\[(1)\Rightarrow 4+2=3y\]\[\Rightarrow y=2\]
الحل:     \((x;y)=(4;2)\)

التمرين 2

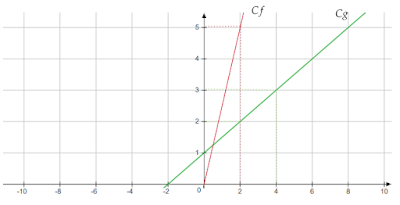
يتضمن التمرين 2 تمثيل مبياني لدالة.

التمرين 2

نعتبر f الدالة الخطية بحيث:       \( f(x)=\frac{5}{2}x\)
  • أحسب:\( f(2)\)
  • لتكن g دالة تالفية بحيث:   \( g(x)=ax+b\) a و b عددان حقيقيات.
  • حدد a و b ععلما أن :   \( g(2)=2\) و \( g(4)=3\)
  • أنشئ التمتيلين المبيانين للدالتين f و g في نفس المعلم المتعامد (O;I;J).

تصحيح التمرين 2، والذي يتضمن تمثيل دالتين على مبيان.

تصحيح التمرين 2
لدينا:                \( f(x)=\frac{5}{2}x\)
1) حساب f(2).
  • لدينا      \( f(x)=\frac{5}{2}x\)
  • إذن       \( f(2)=\frac{5}{2}\times 2\Leftrightarrow f(2)=5\)
  • ومنه     \( f(2)=5\)
2) لنحدد a و b.
  • لدينا:            \( g(x)=ax+b\)
  • وبما أن:      \( a=\frac{g(4)-g(2)}{4-2}=\frac{3-2}{2}=\frac{1}{2}\)
                 \( b=g(2)-a\times 2=2-\frac{1}{2}\times 2=1\)
  • إذن:       \( g(x)=\frac{1}{2}x+1  و b=1  و a=\frac{1}{2}\)
3) التمتيل المبياني للدالتين f و g.
التمتيل المبياني للدالتين g.التمتيل المبياني للدالتين f.
(Cg)xg(x)(Cf)xf(x)
B22O00
C43A25

التمتيل المبياني للدالتين g. التمتيل المبياني للدالتين f.

تمرين 3

تمرين الاحصاء عبر متسلسلة احصائية.

التمرين 3
نعتبر المتسلسلة الاحائية الممثلة بالجدول التالي:
المتسلسلة الاحصائية
قيم الميزة 0 5 10 15 20
الحصيصات 3 2 3 4 8

1) حدد منوال المتسلسلة الاحصائية.
2) أحسب المعدل الحسابي للمتسلسلة الاحصائية.
3) حدد القيمة الوسطية للمتسلسلة الاحصائية.

تصحيح التمرين 3.

تصحيح التمرين 3
1) المنوال:
  • -المنوال هو قيمة (أو صنف) الميزة التي لها أكبر حصيص.
  • أكبر حصيص هو 8 وميزته 8.
  • - إذن المنوال هو الميزة 20.
2) المعدل الحسابي:
\[ m=\frac{(0\times 3)+(5\times 2)+(10\times 3)+(15\times 4)+(20\times 8)}{8+4+3+2+3}\]\[ m=\frac{260}{20}=13\]\[ m=13\]
  • - إذن المعدل الحسابي هو m=13
3) القيمة الوسطية:
  • - نرتب قيم الميزة كالتالي: تصاعديا أو تنازليا.
\[ \underbrace{20.20.20.20.20.20.20.20.15.15}.\underbrace{15.15.10.10.10.5.5.0.0.0}\]\[ \frac{15+15}{2}=15\]
  • - 15 هي القيمة الوسطية.
ملاحظة:
 باستعمال جدول الحصيص المتراكم نجد نفس النتيجة.

تمرين 4

معادلة مختصرة لمستقيم.

التمرين 4

في معلم منسوب الى معلم ممنظم متعامد (O;I;J) ، نعتبر النقطتين A(4;-1) و B(2;3) والمستقيم (D) ذو المعادلة \( y=\frac{1}{2}x-3\)

1) حدد إحداثيتي المتجهة \( \overrightarrow{AB}\) ثم أحسب المسافة AB

2) حدد إحداثيتي M منتصف القطعة [AB].

3) تحقق أن النقطة A تنتمي الى المستقيم (D).

4) حدد المعادلة المختصرة للمستقيم (AB).

5) استنتج أن المستقيمين (D) و (AB) متعامدان.

تصحيح التمرين 4، والذي يتضمن المعادلة المختصرة لمستقيم.

تصحيح التمرين 4

  • - لدينا:  \( (D):y=\frac{1}{2}x-3 ;B(2;3);A(4;-1)\)

1) إحداثيات المتجهة      \( \overrightarrow{AB}\)

\[ \overrightarrow{AB}=(x_{b}-x_{a};y_{b}-y_{a})\]\[ \overrightarrow{AB}=(2-4;3+1)\]\[ \overrightarrow{AB}=(-2;4)\]

  • - المسافة AB

\[ \overrightarrow{AB}=(-2;4)\]\[ AB=\sqrt{(-2)^{2}+4^{2}}\]\[ AB=\sqrt{20}=2\sqrt{5}\]

2) إحداثيات M منتصف (AB)

  • لدينا:   M منتصف (AB)إذن:

\[ M\left ( \frac{{x_{a}+x_{b}}}{2};\frac{y_{a}+y_{b}}{2} \right )\]

  • ومنه:

\[ M\left ( \frac{{4+2}}{2};\frac{-1+3}{2} \right )\]

أي    \( M\left ( 3;1 \right )\)

3) تحقق أن   \( A\in (D)\)

  • لدينا :  \( (D):y=\frac{1}{2}x-3 ;A(4;-1)\)

\[ \frac{1}{2}x_{a}-3=\frac{1}{2}\times 4-3=2-3=-1=y_{a}\]

  • إذن احداثيات A تحقق المعادلة (D).
  • وهذا يعني أن :  \( A\in (D)\)

4) المعادلة المختصرة ل (AB).

ملاحظة:  طريقة مختصرة لتحديد معادلة (AB).

\[ (AB):y=mx+p\]\[ \Leftrightarrow m=\frac{y_{b}-y_{a}}{x_{b}-x_{a}}\]\[  m=y_{a}-mx_{a};p=y_{b}-mx_{b}\]

-إذا كان     \( m_{(AB)}=\frac{a}{b} فإن \overrightarrow{AB}(a;b)\)

لدينا \( \overrightarrow{AB}(-2;4)\)

إذن : \( m(_{AB})=\frac{4}{-2}=-2\)\( p=y_{a}-mx_{a}=-1-(-2)\times 4=7\)

وبالتالي:    \( (AB):y=-2x+7\)

5) استنتاج أن:    \( (AB)\perp (D)\)

ميل (D) هو     \( \frac{1}{2}\) وميل (AB) هو -2.

ولدينا      \( \frac{1}{2}\times(-2)=-1\)

إذن     \( (AB)\perp (D)\)

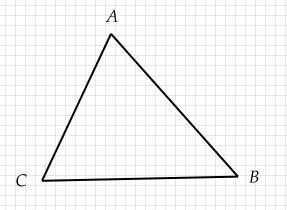
تمرين 5

صورة نقطة بالإزاحة والعلاقات بين المتجهات في المستوى.
التمرين 5
ABC مثلث.
ABC مثلث
1) أنشئ E صورة A بالازاحة التي تحول B الى C.
2) أنشئ النقطة F بحيث: \( \overrightarrow{BF}=-2\overrightarrow{BC}\)
3) بين أن: \( \overrightarrow{CF}=-3\overrightarrow{AE}\)
 تصحيح التمرين هو فرصة لفهم صورة متجهة بالإزاحة، مما يساعد على ترسيخ المفاهيم الرياضية وتعزيز الفهم العميق للمتجهات وكيفية تفاعلها مع بعضها على المبيان.
تصحيح التمرين 5
1) ننشئ E صورة A بالازاحة التي تحول B الى C.
مثلث

2) بين ان: \( \overrightarrow{CF}=-3\overrightarrow{AE}\)
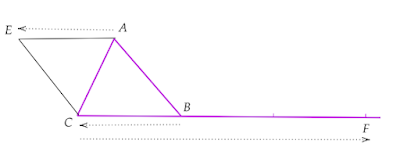
  • -- لدينا   E  صورة A بالازاحة التي تحول B الى C.
  • -- يعني     \( \overrightarrow{BC}=\overrightarrow{AE}\)
3) لدينا    \( \overrightarrow{BF}=-2\overrightarrow{BC}\)
  • -- إذن (علاقة شال)
\[ \overrightarrow{BC}+\overrightarrow{CF}=-2\overrightarrow{BC}\]
\[ \overrightarrow{CF}=-2\overrightarrow{BC}-\overrightarrow{BC}\]
\[ \overrightarrow{CF}=-3\overrightarrow{BC}\]
  • ومنه:      \( \overrightarrow{CF}=-3\overrightarrow{AE}\)

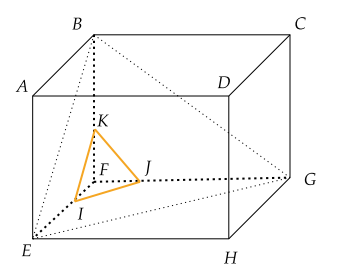
تمرين 6

تمرين في الهندسة الفضائية المستوى الثالث اعدادي.

التمرين 6
ABCDEFGH متوازي مستطيلات قائم بحيث: \( AE=4,5cm وEF=3cm و EH=6cm\)
1) بين أن: \( (AE)\perp (EG)\)
2) أحسب: AG.
3) الهرم KIFG هو تصغير للهرم BEFG  بنسبة  \( k=\frac{1}{3}\)
متوازي مستطيلات قائم

أ- أحسب: V حجم الهرم BEFG.
ب- استنتج:  U حجم الهرم KIFG.

تصحيح التمرين 6، الذي يتضمن حساب حجم هرم، هو فرصة للتمكن من حساب أحجام بعض المجسمات الفضائية.

تصحيح التمرين 6

1) إثبات أن       \( (AE) \perp (EG) \)

  • بما أن \(ABCDEFGH\) متوازي مستطيلات قائم، فإن الأضلاع \( AE \)، \( EF \) و \( EH \) هي أضلاع قائمة الزوايا. لذلك، \( (AE) \perp (EG) \) لأن الزوايا بين الأضلاع قائمة.

2) حساب طول \( AG \)

  • لحساب طول القطر \( AG \) في متوازي المستطيلات القائم، نستخدم نظرية فيثاغورس في الأبعاد الثلاثة: \[ AG = \sqrt{AE^2 + EF^2 + EH^2} = \sqrt{(4.5)^2 + (3)^2 + (6)^2} = \sqrt{65.25} \approx 8.08 \, \text{cm} \]

3) تصغير الهرم \(KIFG\) من \(BEFG\) بنسبة \( k = \frac{1}{3} \)

أ) حساب حجم الهرم \(BEFG\)

  • حجم الهرم: \[ V = \frac{1}{3} \times \text{مساحة قاعدة الهرم} \times \text{الارتفاع} = \frac{1}{3} \times 18 \, \text{cm}^2 \times 4.5 \, \text{cm} = 27 \, \text{cm}^3 \]

ب) حساب حجم الهرم \(KIFG\)

  • بما أن الهرم \(KIFG\) هو تصغير للهرم \(BEFG\) بنسبة \( k = \frac{1}{3} \): \[ U = \left(\frac{1}{3}\right)^3 \times 27 \, \text{cm}^3 = 1 \, \text{cm}^3 \]

شاهد أيضا
- تابعوا المزيد من تصحيح الامتحانات الموحدة المستوى الثالث اعدادي رياضيات، على مدونة المفيد التربوي.
Tags

إرسال تعليق

أحدث أقدم