يعد Dirichlet ( 1805 - 1859 ) من بين الاوائل الذين وضعوا تصورا لمفهوم الدالة كعلاقة تربط بين كل عنصر x بعنصر وحيد y ، دون أن يكون من اللازم التعبير عن هذا الأخير بواسطة متغير x باستعمال عمليات حسابية.
.webp "الدوال العددية")
الدوال العددية les fonctions numériques الجدع المشترك.
فقرات درس الدوال العددية
- - مجموعة تعريف دالة عددية.
- - تساوي دالتين عدديتين.
- - التمثيل المبياني لدالة عددية.
- - الدالة الزوجية والدالة الفردية ( التأويل المبياني).
- - تغيرات دالة عددية.
- - القيم الدنيا والقيم القصوى لدالة عددية على مجال.
1. مجموعة تعريف دالة عددية
عموميات حول الدوال العددية المستوى الثانوي - جدع مشترك.
تعريف 1.
ليكن D جزءا من مجموعة الأعداد الحقيقية R.
نقول إننا عرفنا دالة عددية f على D، إذا ربطنا كل عدد x من D، بعدد حقيقي وحيد يرمز له بالرمز f(x).
المجموعة D تسمى مجموعة تعريف الدالة f .
العدد الحقيقي f(x) يسمى صورة x بالدالة f .
العدد الحقيقي f(x) يسمى صورة x بالدالة f .
تسميات ورموز
الكتابة \[ f:x\mapsto f(x)\] تقرأ الدالة f ، تربط كل عدد x ب f ل x أو f(x).
la fonction ƒ(x) représente l’image de x par ƒ.
أمثلة
مجموعة تعريف الدالة الحدودية (Polynômes) \[ f:x\mapsto 2x^{4}+12x^{3}-5x^{2}+4\] هي: R.
مجموعة تعريف الدالة \[ g:x\mapsto \frac{1}{x}\] هي: \[ ]-\propto ,0[\cup ]0,+\propto[\]
مجموعة تعريف كل من الدالتين: \[ x\mapsto sinx\] و \[ x\mapsto cosx\] هي: R.
ملاحظة
العدد 0 ليست له صورة بالدالة \[ g:x\mapsto \frac{1}{x}\] ، إذا لا يوجد في مجموعة التعريف D.
2. تساوي دالتين
تعريف الدالتين المتساويتين - Égalité de deux fonctions.
تعريف 2
لتكن f و g دالتين عدديتين لمتغير حقيقي x.
نقول إن الدالتين f وg متساويتان إذا كان:
لهما نفس مجموعة التعريف D.
f(x)=g(x) لكل x من D.
f(x)=g(x) لكل x من D.
أمثلة
أ- الدالتان f و g:
f(x)=2(x-2)(x+1) و g(x)=2x²-2x-4 متساويتان تحقق من ذلك.
- مجموعة تعريف الدالة f هي: R.
- مجموعة تعريف الدالة g(x) هي: R.
\[ g(x)=2(x^{2}-x-2)\]
\[ g(x)=2(x^{2}-x-2)\]
\[ g(x)=2(x-2)(x+1)=f(x)\]
- إذن: f(x)=g(x).
ب- \[ f(x)=\frac{x^{2}+x}{x}\] و \[ g(x)=x+1\]
الدالتان f و g غير متساويتين لأن مجموعة تعريف الدالة هي:R-{0}
أما مجموعة تعريف الدالة هي: R.
ملاحظة
يكفي أن نجد عنصرا واحدا a من D حيث: \[ f(a)\neq g(a)\] كي تكون الدالتان f و g غير متساويتان.
إذا وجدنا بعض قيم المتغير x تحقق g(x)=f(x) فهذا غير كاف لتحقيق تساوي f و g.
إذا وجدنا بعض قيم المتغير x تحقق g(x)=f(x) فهذا غير كاف لتحقيق تساوي f و g.
ج- \[ f(x)=\sqrt{x^{2}}\] و \[ g(x)=x\]
f و g غير متساويتين لانه رغم أن لهما نفس مجموعة التعريف R، فإنه يوجد على الأقل عدد من R ليس له نفس الصورة بالدالتين f و g.
g(-1) = -1 و f(-1) = 1 وبالتالي: \[ f(-1)\neq g(-1)\]
3. التمثيل المبياني لدالة عددية
التمثيل المبياني لدالة عددية ( La représentation graphique d'une fonction numérique ).
المستوى P منسوب الى معلم \[ (o,\vec{i},\vec{j})\]
تعريف 3
التمثيل المبياني لدالة عددية f هو مجموعة النقط M(x,y) من المستوى P بحيث y=f(x) و x يتغير في D.
تسميات ورموز
التمثيل المبياني ( la représentation graphique ) لدالة f يسمى ايضا المنحى ( direction ) الممثل للدالة f أو منحى الدالة f، ونرمز له بالرمز C ( courbe ) أو Cf .
- لدينا: \[ Cf=\left\{ M(x,y)\in P/y=f(x);x\in D\right\}\]
\[ M(x,y)\in P\] يعني \[ y=f(x) و x\in D\]
أمثلة
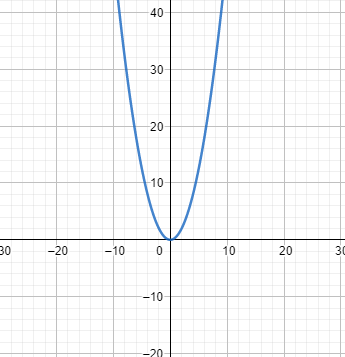
نعتبر الدالة العددية : \[ f(x)=x^{2}+1\]
مجموعة تعريف الدالة f : \[ Df=\mathbb{R}\]
منحى الدالة f:
4. الدالة الزوجية الدالة الفردية
تعريف دالة زوجية ودالة فردية Fonction paire Fonction impaire
تعريف 4
لتكن f دالة عددية و D مجموعة تعريفها.
- نقول إن f دالة زوجية إذا كان لكل x من D: \[ f(-x)=f(x) و (-x)\in D\]
- نقول إن f دالة فردية إذا كان لكل x من D : \[ f(-x)=-f(x) و (-x)\in D\]
أمثلة
نعتبر الدوال العددية: f وg وh لمتغير x حقيقي معرفة على مجموعة تعريف Df.
الدالة f بحيث: f(x)=x دالة فردية.\[ f(-x)=-x=-f(x)\]
الدالة g بحيث: g(x)=x² دالة زوجية.\[ g(-x)=(-x)^{2}=(-1)^{2}x^{2}=g(x)\]
الدالة g بحيث: g(x)=x² دالة زوجية.\[ g(-x)=(-x)^{2}=(-1)^{2}x^{2}=g(x)\]
وبما أن: \[ (-1)^{2}=1\] فإن: \[g(-x)=g(x)\]
5. التأويل المبياني لدالة عددية
التاويل المبياني لدالة عددية - Interprétation graphique d'une fonction numérique.
خاصية 1
f دالة زوجية إذا وفقط إذا كان منحاها في معلم متعامد متماثلا بالنسبة لمحور الأراتب.
خاصية 2
f دالة فردية إذا وفقط إذا كان منحاها في معلم م متماثلا بالنسبة لأصل المعلم.
6. تغيرات دالة عددية
دراسة تغيرات دالة عددية Tableau de variation d'une fonction numérique.
تعريف 5
f دالة عددية و I مجال ضمن مجموعة تعريفها.
- f تزايدية قطعا على I يعني: لكل عنصرين a و b من I إذا كان a<b فإن f(a)<f(b).
- f تناقصية قطعا على I يعني: لكل عنصرين a و b من I إذا كان a<b فإن f(a)>f(b).
- f ثابتة على I يعني: لكل عنصرين a و b من I : فإن f(a)=f(b).
ملاحظة
- - إذا عوضنا f(a)<f(b) ب f(a)≤f(b) نقول إن f دالة تزايدية على I.
- - إذا عوضنا f(a)>f(b) ب f(a)≥f(b) نقول إن f دالة تناقصية على I.
مصطلحات
نقول إن f رتيبة قطعا على I إذا كانت تزايدية قطعا على I أو تناقصية قطعا على I.
نقول إن f رتيبة على I إذا كانت تزايدية على I أو تناقصية على I.
خاصية 3
f دالة ثابتة على مجال I إذا وجد عدد c من R بحيث: f(x)=c لكل x من I .
أمثلة
الدالة العددية f المعرفة على R بمايلي: f(x)=3x تزايدية قطعا على R لأنه لكل a=2 و b=7 من R. 
بما أن: a<b وبما أن f(2)=6 و f(7)=21 ومنه: f(2)<f(7).
الدالة العددية f المعرفة على R بما يلي: f(x)=x²+1.
تزايدية قطعا على \[ [0,+\propto [\] وتناقصية قطعا على \[ ]-\propto ,0 ]\]
7. القيمة الدنيا والقيمة القصوى لدالة عددية على مجال
دراسة القيمة الدنيا والقيمة القصوى لدالة عددية على مجال I.
تعريف 6
لتكن f دالة عددية و I مجالا ضمن مجموعة تعريفها.
نقول إن عددا b هو القيمة القصوى للدالة f على I ، إذا كان b صورة لعدد من I وكان لكل x من I بحيث: f(x) ≤ b.
نقول إن عددا c هو القيمة الدنيا للدالة على f، إذا كان c صورة لعدد من I وكان لكل x من I بحيث: f(x) ≥ c.
نقول إن عددا c هو القيمة الدنيا للدالة على f، إذا كان c صورة لعدد من I وكان لكل x من I بحيث: f(x) ≥ c.
أمثلة
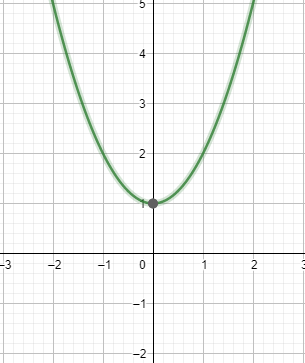
القيمة الدنيا على المجال I=[-4,-4] للدالة f الممثلة بالمنحى جانبه هي العدد 2.
وتأخذها الدالة f عندما يكون x=0.
القيمة القصوى على المجال I=[-4,4] للدالة f هي العدد 0.
وتأخذها الدالة f عندما يكون x=0.
ملاحظة
f(0)=2 هي القيمة الدنيا للدالة f على المجال I، يعني أن 2 هي أصغر قيمة تأخذها f(x) على I .
f(0)=0 هي القيمة القصوى للدالة f على المجال I، يعني أن 0 هي أكبر قيمة تأخذها f(x) على I .
f(0)=0 هي القيمة القصوى للدالة f على المجال I، يعني أن 0 هي أكبر قيمة تأخذها f(x) على I .
استثمار التعلمات
سلسلة تمارين درس الدوال العددية مع التصحيح، خيار علمي عربية وعلمي فرنسية.
| سلسلة تمارين خيار عربية | سلسلة تمارين خيار فرنسية | ||
|---|---|---|---|
| سلسلة 1 | تحميل | سلسلة 1 | تحميل |
| سلسلة 2 | تحميل | سلسلة 2 | تحميل |
| سلسلة 3 | تحميل | سلسلة 3 | تحميل |
| سلسلة 4 | تحميل | سلسلة 4 | تحميل |
| سلسلة 5 | تحميل | سلسلة 5 | تحميل |
Tags
ملخصات ودروس