المجموعات N و Z و D و Q و R جدع مشترك

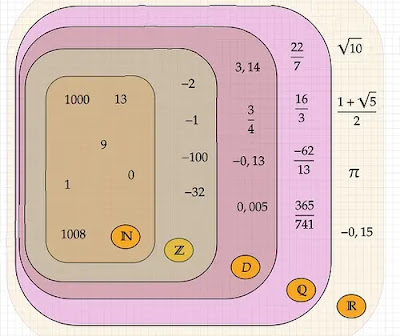
في مجال الرياضيات، وتحديديا في المستوى الثانوين الجدع مشترك، هناك خمس مجموعات أساسية تسمح لنا بمعالجة الأرقام والحساب الحرفي.
يمكن أن تكون هذه المجموعات متممة لما سبقها من مجموعة، مثلا المجموعة Z هي مثممة للمجموعة N.
وتختلف أيضًا في أنواع الأرقام التي تحتوي عليها.
إن دراسة هذه المجموعات من الأصغر إلى الأكبريساعدنا في تحديد وتقديم كل مجموعة على حدة، بل أيضًا يمكننا في فهم الاختلافات بينها من خلال أمثلة توضيحية.

 المجموعات N و Z و D و Q و R.

مجموعات الأعداد N و Z و D و Q و R المستوى الثانوي اعدادي

 يتوخى من هذا الدرس المستوى الثانوي جدع مشترك، التمييز بين مختلف أنواع الأعداد الاساسية في الحساب الحرفي، واعتماد ترميز خاص بكل مجموعة ثم ادراك العلاقات التي تربط بين هذه الأعداد.

فقرات الدرس
المجموعات Z و D و Q و R: كتابة وترميز.
أ) مجموعة الأعداد الصحيحة النسبية Z.
ب) مجموعة الاعداد العشرية النسبية D
د) مجموعة الأعداد الحقيقية R .
ج) مجموعة الأعداد الجذرية Q.
استثمار وتقويم التعلمات

1. المجموعات Z و D و Q و R كتابة وترميزالمجموعات

التعرف على المجموعات Z و D و Q و R كتابة وترميز.

أ) مجموعة الأعداد الصحيحة النسبية Z.

تعريف 1

الأعداد الصحيحة الطبيعية ومقابلاتها تكون مجموعة تسمى مجموعة الأعداد الصحيحة النسبية.
 ويرمز لها بالرمز Z.

أمثلة

 .. 3 ، 2 ، 1 ، 0 ، -1 ، -2 ، -3 ، ... أعدادا صحيحة نسبية.

 نقول ان  ( -3 )عنصر من Z او ( -3 ) ينتمي الى Z ونكتب \[ (-3)\in \mathbb{Z}\]

 الاعداد \[ 0,12  و \frac{5}{11}  و \sqrt{3}\] ليست اعداد صحيحة نسبية.

 نكتب: \[ \frac{5}{11}\notin \mathbb{Z}\]

ملاحظة
 كل عدد صحيح طبيعي هو عدد صحيح.
 نقول إن المجموعة N جزء من المجموعة Z او المجموعة N ضمن المجموعة Z ونكتب \[ \mathbb{N}\subset \mathbb{Z}\]

ب) مجموعة الاعداد العشرية النسبية D

التعرف على مجموعة الاعداد العشرية النسبية D.

تعريف 2

كل عدد له كتابة كسرية على شكل \[ \frac{a}{10^{n}}\] حيث \[ a\in \mathbb{\mathbb{Z}}...n\in \mathbb{N}\] ، يسمى عددا عشريا نسبيا.

تسميات ورموز

يرمز لمجموعة الأعداد العشرية النسبية بالرمز D.

نتائج

1. العدد العشري له كتابة بعدد منته من الأرقام على يمين الفاصلة.
2.  كل عدد صحيح نسبي

1. a هو عدد عشري نسبي، لأنه يمكن كتابته على شكل \[ \frac{a}{10^{0}}\]

إذن: \[ \mathbb{N\subset \mathbb{Z\subset }D}\]

أمثلة

\[ 7,005;\frac{3}{4};-\frac{5}{7};-0,03;2004;-4;6\]

ج) مجموعة الأعداد الجذرية Q.

التعرف على مجموعة الأعداد الجذرية Q.

العدد الجذري هو كل عدد يمكن كتابته على شكل \[ \frac{a}{b}\] حيث a و b عددان صحيحان نسبيان مع \[ b\neq 0\]

تسميات ورموز

 يرمز لمجموعة الأعداد الجذرية بالرمز Q.

أمثلة

الاعداد \[ \frac{1}{3},\frac{0,5}{7},\frac{10^{-5}}{10^{3}}\] هي أعداد جذرية.

 

نتيجة

 كل عدد عشري نسبي هو عدد جذري.
لان: \[ \frac{a}{10^{n}}=\frac{a}{b}\] حيث: \[ n\in \mathbb{N}  وb=10^{n}\]
إذن: \[ \mathbb{N\subset \mathbb{Z\subset D\subset \mathbb{Q}}}\]

د) مجموعة الأعداد الحقيقية R .

توجد مقادير لا يمكن التعبير عنها بأعداد جذرية، مثل هذه المقادير نعبرعنها بأعداد تسمى أعدادا لا جذرية.

مثال

 طول قطر مربع ضلعه 1 هو عدد لا جذري.

 نصف محيط دائرة شعاعها 1 هو عدد لا جذري يرمز له بالرمز π.

تعريف 4

الأعداد الجذرية والاعداد اللاجذرية تكون مجموعة تسمى مجموعة الأعداد الحقيقية و يرمز لها بالرمز R.

مثال

الأعداد: \[ 5\pi ^{2},\frac{0,5}{11},5^{3},\sqrt{3},...\] هي أعدادا حقيقية.

نتيجة

كل عدد جذري فهو عدد حقيقي.

إذا: \[ \mathbb{N\subset \mathbb{Z\subset D\subset \mathbb{Q\subset \mathbb{R}}}}\]

 تمثيل المجموعة R.

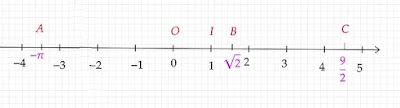
 تمثيل المجموعة R بمستقيم مدرج (O,I)Δ.

- كل نقطة من هذا المستقيم تقبل عددا حقيقيا وحيدا أفصولا لها.
- وكل عدد حقيقي هوأفصول لنقطة وحيدة من هذا المستقيم.

 نكتب A(-π) ونقرأ A هي النقطة ذات الأفصول (-π).

2. العمليات في المجموعة  R وخاصياتها

عمليات في الجمع والضرب في مجموعة الاعداد الحقيقية R وخاصياتها .

أ. الجمع والضرب

لكل a و b و c  و d من R  لدينا:

\[a+b=b+a \]\[a+(b+c)=(a+b)+c \]\[(-a)+a=0 \]\[ab=ba \]\[a(bc)=(ab)c \]\[(a\neq 0)a\times\frac{1}{a}=1 \]\[a(b+c)=ab+ac \]

ب. قواعد الحساب في R

لكل a و b و c و d من R لدينا:
\[a=c-b\Leftrightarrow a+b=0\]
\(b=0\) أو \(a=0\)تكافئ \[ab=0\]
\[a=b\]تكافئ \[ac=bc(c\neq 0)\]\[\frac{a}{b}=a\times\frac{1}{b}(b\neq 0)\]

لتكن a وb وc وd أعدادا حقيقية لدينا:\[(b\neq 0)\;;-\frac{a}{b}=\frac{-a}{b}=\frac{a}{-b}\]
\[(d\neq 0)\;(b\neq 0)\;ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\]
إذا كان:
\[(b\neq 0)\;(d\neq 0)\;\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}\]

إذا كان: 

\[\frac{1}{\frac{a}{b}}=\frac{b}{a}\;(a\neq 0);(b\neq 0)\]

إذا كان: 

\[\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{ad}{bc}\;;(b\neq 0)(c\neq 0)(d\neq 0)\]

ج. الجذور المربعة

تعريف 3

ليكن a عددا حقيقيا موجبا.

الجذر المربع للعدد هو العدد الموجب الذي مربعه يساوي a .

مثال

نرمز للجذر المربع لعدد a \((a\geq 0) \) بالرمز \(\sqrt{a}\)

\[(\sqrt{5});\sqrt{10};\sqrt{131};\sqrt{665})\]

نتائج

إذا كان a موجبا فإن \[\sqrt{a^{2}}=a\]

إذا كان a سالبا فإن \[\sqrt{a^{2}}=-a\]

لكل عددين حقيقيين موجبين a وb :

\[\sqrt{ab}=\sqrt{a}\sqrt{b}\]\[\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\;(b\neq 0)\]\[b=\sqrt{a}\Leftrightarrow b^{2}=a\]\[a=b\Leftrightarrow\sqrt{a}=\sqrt{b}\]

أمثلة

\[\sqrt{4}=2\;;-\sqrt{4}=-2 \]\[\sqrt{\frac{3}{7}}=\frac{\sqrt{3}}{\sqrt{7}}\;;\sqrt{12}=\sqrt{3}\sqrt{4}\]

عموما

\[\sqrt{3+5}\neq\sqrt{3}+\sqrt{5}\]

ملاحظة

لكل عدد a حقيقي موجب يوجد عددان حقيقيان مربعهما يساوي  \[-\sqrt{a}\] و \[\sqrt{a}\]

3. قوى عدد عشري

تعريف 4

ليكن a عدد n و عددا صحيح طبيعيا منعدم.

\[(a\neq 0)\;a^{-n}=\frac{1}{a^{n}}\] 

\[ a^{n}=\underbrace{a\times a\times...\times a}\]

حالات خاصة

 إذا كان\[ a\neq 0\]

 فإن\[a^{0}=1\]

قوى العدد 10\[10^{-6}=\underbrace{0,00000}1\]\[10^{4}=1\underbrace{0000}\]

نتائج

ليكن  a و b عددين حقيقيين غير منعدمين وليكن n و m عددين صحيحين نسبيين 

\[(1)\;: a^{-n}=(\frac{1}{a})^{n}\]\[(2)\;: a^{n}\times a^{m}=a^{n+m}\]\[(3)\;: (a^{m})^{n}=a^{mn}\]\[(4)\;: \frac{a^{m}}{a^{n}}=a^{m-n}\]\[(5)\;: \sqrt{a^{n}}=(\sqrt{a})^{n}\;(a> 0) \]\[(6)\;: (ab)^{n}=a^{n}b^{m}\]\[(7)\;: (\frac{a}{b})^{n}=\frac{a^{n}}{b^{n}}\]

أ. الكتابة العلمية لعدد عشري

خاصية 1

كل عدد عشري b موجب يكتب على شكل

\[a\times 10^{p}\]

حيث p عدد صحيح نسبي و a عدد عشري يحقق

\[1\leq a< 10\]

أمثلة
هذه الكتابة تسمى الكتابة العلمية للعدد العشري b .
الكتابة العلمية للعدد 8734200000 هي \[8,7342\times 10^{9}\]
الكتابة العلمية للعدد 0,0000125 هي\[1,25\times 10^{-5}\]

نتيجة

كل عدد عشري سالب يكتب على شكل

\[(-a10^{p})\]

 حيث p  عدد صحيح نسبي و a عدد عشري يحقق

\[1\leq a< 10\]

مثال
\[-17351=-1,7351\times 10^{+4}\]
\[-0,12=-1,2\times 10^{-1}\]

4. المتطابقات الهامة

لكل a و b  من R لدينا:

\[(a+b)^{2}=a^{2}+2ab+b^{2}\]\[(a-b)^{2}=a^{2}-2ab+b^{2}\]\[a^{2}-b^{2}=(a-b)(a+b)\]\[a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\]\[a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\]

5. النشر والتعميل

تعريف 5

نشر مجموع هو تحويله الى جداء.

تعميل مجموع هو تحويله الى جذاء.

مثال

\[ 10\times (25+2,56)=10\times 25+10\times 2,56\]\[(26\times 37)+(26\times 158)=26\times (37+158)\]

تقويم التعلمات

استثمار سلسلات ومسائل 

تحميل ومعاينة سلسلات تمارين ومسائل درس مجموعات الاعداد جدع مشترك المستوى الأولى ثانوي.
سلسلة تبسيط وتعميل تعابير أعداد حقيقية، انجاز عمليات في المجموعة R، القوى وخاصياتها، الكتابة العلمية لعدد عشري، استعمال المحسبة.

سلسلة تمارين خيار عربية		سلسلة تمارين خيار فرنسية
سلسلة 1	تحميل	سلسلة 1	تحميل
سلسلة 2	تحميل	سلسلة 2	تحميل
سلسلة 3	تحميل	سلسلة 3	تحميل
سلسلة 4	تحميل	سلسلة 4	تحميل
سلسلة 5	تحميل	سلسلة 5	تحميل
سلسلة 6	تحميل	سلسلة 6	تحميل